一、考察频率以及难度
考察频率:⭐⭐⭐
笔试题难度:⭐⭐⭐⭐⭐
算法难度:⭐⭐⭐⭐⭐
一般作为笔试的压轴题出现。
二、学习技巧
对于递归逻辑清楚。
掌握常见的树形dp的状态推导。
三、应用场景
给定一个无向无环图(树),求树上的一些操作可以获得的最大价值、最小价值以及方案数。
四、算法讲解
树形动态规划(Tree DP)是一种常规动态规划在树这种特殊数据结构上的一种应用。其本质还是动态规划,只不过状态和选择有些特殊。
对于树形动态规划,状态的定义通常有一个关键的特点,那就是选择了某个节点后,其子树内的所有节点自动被选择。这种性质就导致了状态和选择之间的关系必然会受到树的树形结构的影响,从而产生了一种更为复杂的状态转移方程。
五、例题与解析
习题1 最大的维护成本
https://oj.niumacode.com/problem/P1114
由于软件技术的提升,原有部署网络中某些节点可以撤掉,这样可以简化网络节省维护成本。但是要求撤掉网络节点时,不能同时撤掉原来两个直接相互连接的节点。输入的网络是一个满二叉树结构,每个网络节点上标注一个数值,表示该节点的每年维护成本费用。给定每个输入网络,按照要求撤掉某些节点后,求出能够节省的最大的维护成本。
输入
第一行:一个正整数N,表示后面有N个数值。1<=N<= 10000 第二行:N个非负整数,表示网络节点每年的维护成本,按照满二又树的”广度优先遍历序号”给出。0表示不存在该关联节点,0只会存在于叶子节点上。每个数字的取值范围为[0.1000]
输出
能够节省的最大的维护成本。
样例输入:
7
5 3 5 0 6 0 1样例输出
12题目解析
这道题我们抛开背景后,起始就是找到若干个不相邻的节点,使得其总和最大。
那么我们可以用动态规划的思想进行分析:每个节点都有2种选择:选和不选。我们对于每个节点的选择取其最优解即可。
定义状态:f[i][0] 不选择第i个节点,f[i][1]选择第i个节点。
转移:
f[i][0] = Σmax(f[j][0], f[j][1]),其中j是i的子节点,表示如果第i个节点不选择,那么孩子节点可以选也可以不选。
f[i][1] = Σ(f[j][0]) + val[i],其中j是i的子节点,表示如果第i个节点选择了,那么子节点只能不选。
按照递归后序遍历方式,完成dp表格的填写即可。(一般树形dp的填表都是通过递归后序遍历完成,因为一般都是父节点依赖子节点,所以需要保证我们填写父节点状态的时候,子节点状态已经填完了)。
C++代码
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int n;
vector<int> val;
vector<vector<int>> f;
void dfs(int i) {
if (i >= n || val[i] == 0) return;
dfs(2*i + 1);
dfs(2*i + 2);
int left = 2*i + 1, right = 2*i + 2;
f[i][0] = max(f[left][0], f[left][1]) + max(f[right][0], f[right][1]);
f[i][1] = f[left][0] + f[right][0] + val[i];
}
int main() {
cin >> n;
val.resize(n);
f.resize(2*n+2, vector<int>(2));
for(int i = 0; i < n; ++i) cin >> val[i];
dfs(0);
cout << max(f[0][0], f[0][1]) << endl;
return 0;
}Java
import java.util.Scanner;
public class Main {
static int n;
static int[] val;
static int[][] f;
static void dfs(int i) {
if (i >= n || val[i] == 0) return;
dfs(2*i + 1);
dfs(2*i + 2);
int left = 2*i + 1, right = 2*i + 2;
f[i][0] = Math.max(f[left][0], f[left][1]) + Math.max(f[right][0], f[right][1]);
f[i][1] = f[left][0] + f[right][0] + val[i];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
val = new int[n];
f = new int[n][2];
for(int i = 0; i < n; ++i) val[i] = scanner.nextInt();
dfs(0);
System.out.println(Math.max(f[0][0], f[0][1]));
}
}Python
n = int(input())
val = [int(c) for c in input().split()]
f = [[0]*2 for _ in range(2*n+2)]
def dfs(i):
if i>=n or val[i]==0: return
dfs(i * 2 + 1)
dfs(i * 2 + 2)
left,right = i * 2 + 1, i * 2 + 2
f[i][0] = max(f[left][0], f[left][1]) + max(f[right][0], f[right][1])
f[i][1] = f[left][0] + f[right][0] + val[i]
dfs(0)
print(max(f[0][0], f[0][1]))习题2 在树上执行操作以后得到的最大分数
https://oj.niumacode.com/problem/P1115
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 ,根节点编号为 0 。给你一个长度为 n - 1 的二维整数数组 edges 表示这棵树,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个长度为 n 下标从 0 开始的整数数组 values ,其中 values[i] 表示第 i 个节点的值。
一开始你的分数为 0 ,每次操作中,你将执行:
选择节点 i 。
将 values[i] 加入你的分数。
将 values[i] 变为 0 。
如果从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0 ,那么我们称这棵树是 健康的 。
你可以对这棵树执行任意次操作,但要求执行完所有操作以后树是 健康的 ,请你返回你可以获得的 最大分数 。
示例 1:
输入
6
0 1
0 2
0 3
2 4
4 5
5 2 5 2 1 1输出
11解释
我们可以选择节点 1 ,2 ,3 ,4 和 5 。根节点的值是非 0 的。所以从根出发到任意叶子节点路径上节点值之和都不为 0 。所以树是健康的。你的得分之和为 values[1] + values[2] + values[3] + values[4] + values[5] = 11 。
11 是你对树执行任意次操作以后可以获得的最大得分之和。示例 2:
输入
7
0 1
0 2
1 3
1 4
2 5
2 6
20 10 9 7 4 3 5输出
40解释
我们选择节点 0 ,2 ,3 和 4 。
- 从 0 到 4 的节点值之和为 10 。
- 从 0 到 3 的节点值之和为 10 。
- 从 0 到 5 的节点值之和为 3 。
- 从 0 到 6 的节点值之和为 5 。
所以树是健康的。你的得分之和为 values[0] + values[2] + values[3] + values[4] = 40 。
40 是你对树执行任意次操作以后可以获得的最大得分之和。提示:
2 <= n <= 2 * 10^4
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
values.length == n
1 <= values[i] <= 10^9
输入保证 edges 构成一棵合法的树。
题目解析
由于题目要求的是从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0。因此,某一条路径上已经没有把一个节点放入自己的分数,那么这个子树的所有节点价值都可以加入到自己的分数。
我们定义
dp[i][0]:以i为根的子树,需要保留一个节点不加入自己的分数的最大收益。
dp[i][1]:以i为根的子树,不需要保留节点可以获取的最大收益。
推导如下:
dp[i][0] = MAX(保留这个节点,不保留这个节点)
其中:保留这个节点=Σdp[child][1].
不保留这个节点 = value[node] + dp[child][0]
dp[i][1] =values[node] + Σdp[child][1]
C++
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int MAXN = 100005;
int n;
vector<int> graph[MAXN];
int values[MAXN];
int dp[MAXN][2];
void dfs(int node, int fa) {
dp[node][0] = 0;
int kp = 0, not_kp = values[node];
dp[node][1] = values[node];
for (int next : graph[node]) {
if (next != fa) {
dfs(next, node);
dp[node][1] += dp[next][1];
kp += dp[next][1];
not_kp += dp[next][0];
}
}
if (graph[node].size() != 1 || node == 0) {
dp[node][0] = max(kp, not_kp);
}
}
int main() {
cin >> n;
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 0; i < n; i++) {
cin >> values[i];
}
memset(dp, 0, sizeof(dp));
dfs(0, -1);
cout << dp[0][0] << endl;
return 0;
}Java
import java.util.*;
public class Main {
static final int MAXN = 100005;
static int n;
static List<Integer>[] graph = new ArrayList[MAXN];
static int[] values = new int[MAXN];
static int[][] dp = new int[MAXN][2];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < n - 1; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
for (int i = 0; i < n; i++) {
values[i] = sc.nextInt();
}
dfs(0, -1);
System.out.println(dp[0][0]);
}
static void dfs(int node, int fa) {
dp[node][0] = 0;
int kp = 0, not_kp = values[node];
dp[node][1] = values[node];
for (int next : graph[node]) {
if (next != fa) {
dfs(next, node);
dp[node][1] += dp[next][1];
kp += dp[next][1];
not_kp += dp[next][0];
}
}
if (graph[node].size() != 1 || node == 0) {
dp[node][0] = Math.max(kp, not_kp);
}
}
}Python
rom collections import defaultdict
from typing import List
n = int(input())
edges = []
for _ in range(n-1):
a,b = map(int, input().split())
edges.append((a,b))
values = [int(c) for c in input().split()]
graph = defaultdict(list)
for a, b in edges:
graph[a].append(b)
graph[b].append(a)
# n = len(graph)
dp = [[0] * 2 for _ in range(n)]
def dfs(node, fa):
dp[node][0] = 0
kp, not_kp = 0, values[node]
dp[node][1] = values[node]
for next in graph[node]:
if next != fa:
dfs(next, node)
dp[node][1] += dp[next][1]
kp += dp[next][1]
not_kp += dp[next][0]
if len(graph[node]) != 1 or node == 0: dp[node][0] = max(kp, not_kp)
dfs(0, -1)
print(dp[0][0])习题3 子树中标签相同的节点数
https://oj.niumacode.com/problem/P1117
给你一棵树(即,一个连通的无环无向图),这棵树由编号从 0 到 n - 1 的 n 个节点组成,且恰好有 n - 1 条 edges 。树的根节点为节点 0 ,树上的每一个节点都有一个标签,也就是字符串 labels 中的一个小写字符(编号为 i 的 节点的标签就是 labels[i] )
边数组 edges 以 edges[i] = [ai, bi] 的形式给出,该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组,其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
示例 1:
输入
7
0 1
0 2
1 4
1 5
2 3
2 6
abaedcd输出
2 1 1 1 1 1 1释放
节点 0 的标签为 'a' ,以 'a' 为根节点的子树中,节点 2 的标签也是 'a' ,因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ,节点 1 的子树包含节点 1、4 和 5,但是节点 4、5 的标签与节点 1 不同,故而答案为 1(即,该节点本身)。示例 2:
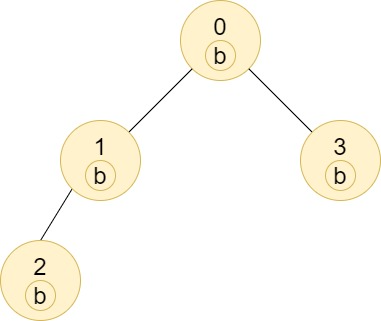
输入
4
0 1
1 2
0 3
bbbb输出
4 2 1 1解释
节点 2 的子树中只有节点 2 ,所以答案为 1 。
节点 3 的子树中只有节点 3 ,所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ,标签都是 'b' ,因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3,标签都是 'b',因此答案为 4 。示例 3:
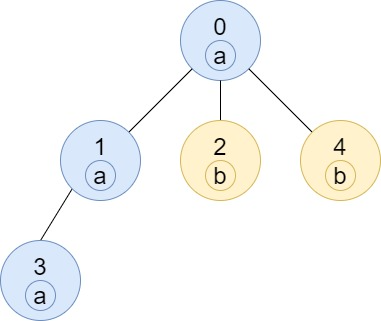
输入
5
0 1
0 2
1 3
0 4
aabab输出
3 2 1 1 1提示:
1 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
labels.length == n
labels 仅由小写英文字母组成
题目解析
树形dp。
dfs(u,f)会返回的是:以u为根的子树,每个字母的数量。
那么此时的转移自然就是 cnt[i] += sub[i],其中i∈[0,25],且sub是u的所有子节点的返回。
C++
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
using namespace std;
const int MAXN = 100005;
vector<int> graph[MAXN];
int ans[MAXN];
string labels;
vector<int> dfs(int u, int f) {
vector<int> cnt(26, 0);
cnt[labels[u] - 'a']++;
for (int v : graph[u]) {
if (v == f) continue;
vector<int> sub = dfs(v, u);
for (int c = 0; c < 26; c++) {
cnt[c] += sub[c];
}
}
ans[u] = cnt[labels[u] - 'a'];
return cnt;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
cin >> labels;
dfs(0, -1);
for (int i = 0; i < n; i++) {
cout << ans[i] << " ";
}
cout << endl;
return 0;
}Java
import java.util.*;
public class Main {
static final int MAXN = 100005;
static List<Integer>[] graph = new ArrayList[MAXN];
static int[] ans = new int[MAXN];
static String labels;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < n - 1; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph[a].add(b);
graph[b].add(a);
}
labels = sc.next();
dfs(0, -1);
for (int i = 0; i < n; i++) {
System.out.print(ans[i] + " ");
}
System.out.println();
}
static int[] dfs(int u, int f) {
int[] cnt = new int[26];
cnt[labels.charAt(u) - 'a']++;
for (int v : graph[u]) {
if (v == f) continue;
int[] sub = dfs(v, u);
for (int c = 0; c < 26; c++) {
cnt[c] += sub[c];
}
}
ans[u] = cnt[labels.charAt(u) - 'a'];
return cnt;
}
}Python
n = int(input())
edges = []
for _ in range(n-1):
a,b = map(int, input().split())
edges.append((a,b))
labels = input()
graph = [[] for _ in range(n)]
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
ans = [0] * n
def dfs(u,f):
cnt = [0] * 26
cnt[ord(labels[u]) - ord('a')] += 1
for v in graph[u]:
if v == f:continue
sub = dfs(v,u)
for c in range(26):
cnt[c] += sub[c]
ans[u] = cnt[ord(labels[u]) - ord('a')]
return cnt
dfs(0,-1)
print(ans)六、常见陷阱
状态定义不清晰,容易搞混。
状态转移关系混乱,推导出错。